Description

First of all I would like to emphesize that please feel free to contribute and to correct all my mistakes, There is plenty of space that the approach could be optimized and generalized.

The Raft consensus algorithm is typically used for achieving consensus in distributed systems, particularly in applications like distributed databases and configuration management. Applying Raft to dynamical systems such as robots can be beneficial in certain scenarios. For example, if you have a group of robots that need to coordinate their actions and maintain a consistent state, Raft could help ensure that all robots agree on the state of the system and the actions to be taken. This can be particularly useful in environments where communication is unreliable, or where there is a risk of individual robot failures.

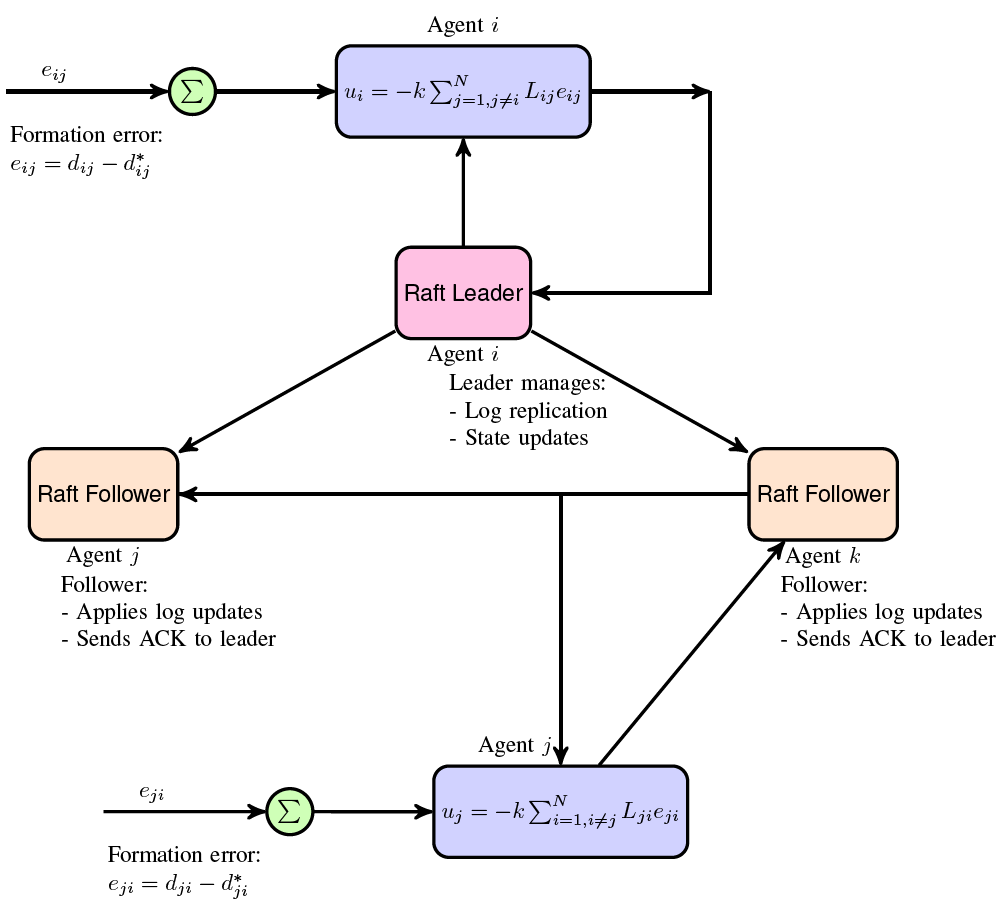
The Raft consensus algorithm is not used to solve the formation control problem in a traditional sense. Instead, it is used to synchronize the states (i.e., positions) of the agents across different nodes in a distributed system. We assume that each agent is on a different node in the Raft algorithm. In this case, each agent will be managed by a separate node in the Raft cluster, and these nodes will use the Raft algorithm to reach a consensus on the agents’ states. When each agent is on a separate node, it means that each agent’s state is managed independently within its associated node. The Raft algorithm is responsible for ensuring that the agent’s state is consistent across all nodes. This will allow the agents to cooperate and reach the desired formation on a regular polygon.

Here is a schematic shows the integration of Raft consensus algorithm with formation control of multi-agent systems. Integration of the Raft communication steps:

• Agent \(i\) updates its position \(\boldsymbol{x}_i\) and/or control input \(\boldsymbol{u}_i\), and sends the update to the Raft leader.

• The Raft leader appends the update to its log and replicates the log to all followers.

• Followers receive the log, apply updates to their state machines, and send acknowledgments back to the leader.

• The leader ensures a majority of agents have applied the update before considering it committed.

Scenario A

In Scenario A, the Raft algorithm ensures system continuity by electing a new leader if the current one disconnects. Nodes vote for a new leader based on unique identifiers. The code snippet below, part of a larger simulation, illustrates a crucial function where the leader updates the positions of all agents, demonstrating the system’s core logic amidst leader transitions.

def leader_update(formation_obj):
    # Calculating new positions for all agents
    new_positions = [
        single_integrator_dynamics(formation_obj, i, formation_obj.goals[i])
        for i in range(len(formation_obj.agents))
    ]
    # Updating all agents with their new positions
    formation_obj.update_all_agents(new_positions)

In this code, leader_update computes new positions for all agents, which are then updated through the update_all_agents method, ensuring the system’s coherent operation.

Scenario B

In scenario B, when a leader agent or node fails at a specific time, its position ceases to update, indicating disconnection. Despite this, the remaining agents reorganize into a regular n-sided polygon formation. The code snippet below is crucial as it calculates and updates the positions of active agents, ensuring the maintenance of the formation even in the event of leader failure.

def leader_update(formation_obj, active_agents):
    new_positions = [
        single_integrator_dynamics(formation_obj, i, formation_obj.goals[i])
        for i in active_agents
    ]

    for i, new_position in zip(active_agents, new_positions):
        formation_obj.update_agent(i, new_position)

def update_frame(frame_number):
    active_agents = get_active_agents(distributed_formation_objects)
    leader_index = active_agents[(frame_number // 20 + distributed_formation_objects[0].leader_offset) % len(active_agents)]
    leader_node = distributed_formation_objects[leader_index]

    # ... rest of the code ...
    
    if leader_node._isReady():
        leader_update(leader_node, active_agents)
    # ... rest of the code ...

In the leader_update function, new positions are computed for each active agent based on a predefined dynamics model, and then updated. The update_frame function conducts the simulation frame by frame, managing leader failure and the subsequent new leader election, ensuring the continuation of the agent formation even in the face of leader disconnection.

Scenario C

In this scenario, when an agent or nodes fails as a leader at a specific time, the position of the failed leader should not be updated anymore showing that the agent is disconnected from the rest. the snippet below demonstrates how the position of a failed leader agent is not updated after a specific frame (in this case, frame 35), indicating a disconnection:

def update_frame(frame_number):
    ...
    # Simulate leader failure at frame 35 and log the event
    if frame_number == 35:
        leader_node.failed = True
        print(f"Frame {frame_number}: Leader (Agent {leader_index}) failed")
        for formation_obj in distributed_formation_objects:
            formation_obj.leader_history.append({"type": "failure", "leader": leader_index, "time": frame_number})
    ...
    if leader_node._isReady():
        leader_update(leader_node, active_agents)
    ...

Other Scenarios

Over time I try to complete the post here, yet you have access to both the paper and the source code.